Region of Practical Equivalence (ROPE)

A/B Tests by design have an annoying habit that you will realize as you attain maturity in experimentation. As explained in the previous article, the minimum detectable effect drops monotonically as sample sizes are increased. In other words, as you add more samples to the study you are able to get significance for smaller and smaller uplifts. Theoretically, any test with infinite samples will always result in significance because no two means are ever exactly the same. It quickly becomes annoying because if you don't stop your urge to add samples to your study most of your tests would come out to be significant but with a very small uplift. The paradox quickly boils down to choosing the boundary between incremental and meaningful improvements.

The real world does not hail every minute improvement you make. Sometimes, the cost of implementing a feature exceeds the uplift to justify its launch. Most digital experimenters would not consider deploying a change smaller than 3-5% of their base conversion rate. They say that these differences appear by chance and might not actually stick long enough in the future. But, traditional hypothesis tests give you an option to test for better or worse but never for equivalence. Insignificance only lets you know that the change was not large enough to be detectable in the given sample size.

Region of Practical Equivalence (ROPE) is a theoretical construct to mitigate this annoying habit of A/B tests. On the axis of improvement, ROPE lets you define a region around 0, where differences are not worth implementing and hence requires significance to be adjusted accordingly. In other words, if an improvement below 2% is not worth implementing for you, then a 95% chance that improvement > 0 might translate to only 66% chance that the improvement is greater than 2%. Would you want to deploy a change which has a 66% chance that it will justify your costs of implementation? You should rather want a 95% guarantee that your improvement will be greater than 2%.

The discussion on ROPE is tricky and I am at a stage where I am learning the nuances of ROPE. ROPE is debatable because proponents of statistical power would quickly tell you that if you calculate significance just once after the required sample sizes are reached, insignificance will practically translate to equivalence as well. The discussion then devolves to the fact that why invent new statistical jargon when Minimum Detectable Effect is already capturing that dimension of A/B Testing. Finally, it leads us to the insidious question, are ROPE and MDE actually the same thing? Or not?

I will try to answer this question according to my present understanding in this blog. I am open to new perspectives on this discussion and will keep this article updated as I learn new things about ROPE (or invalidate my current understanding).

Deepening the dichotomy

If you start to think about MDE and ROPE, you observe that both of these metrics define a region around 0 improvement that restricts declaring any variation below a certain improvement to be a winner (significant). MDE and ROPE sound like the same thing in that regard and hence you feel that you can either justify the limitation with sample sizes (MDE) or with implementation costs (ROPE), the implication is the same. However, there is a fundamental difference I see between ROPE and MDE.

MDE is a limitation of experimentation and the number of sample sizes you want to devote to the study. Sample Sizes that you want to invest in the test might vary with the priority of the change or the expected timeline of the launch. However, the ROPE of a goal is a more uniform metric of interest. A conversion rate uplift of less than 2% might not make sense irrespective of what experiment you are running because overhead costs are too much. There might be cases where the constraints of experimentation are much more than the constraints of implementation due to a lack of traffic.

The question arises can we consider ROPE to be equal to MDE for all those cases where sample sizes are not enough to test at the desired implementational limits? The answer is that ROPE is still slightly different.

Calibrating Significance to the New Baseline

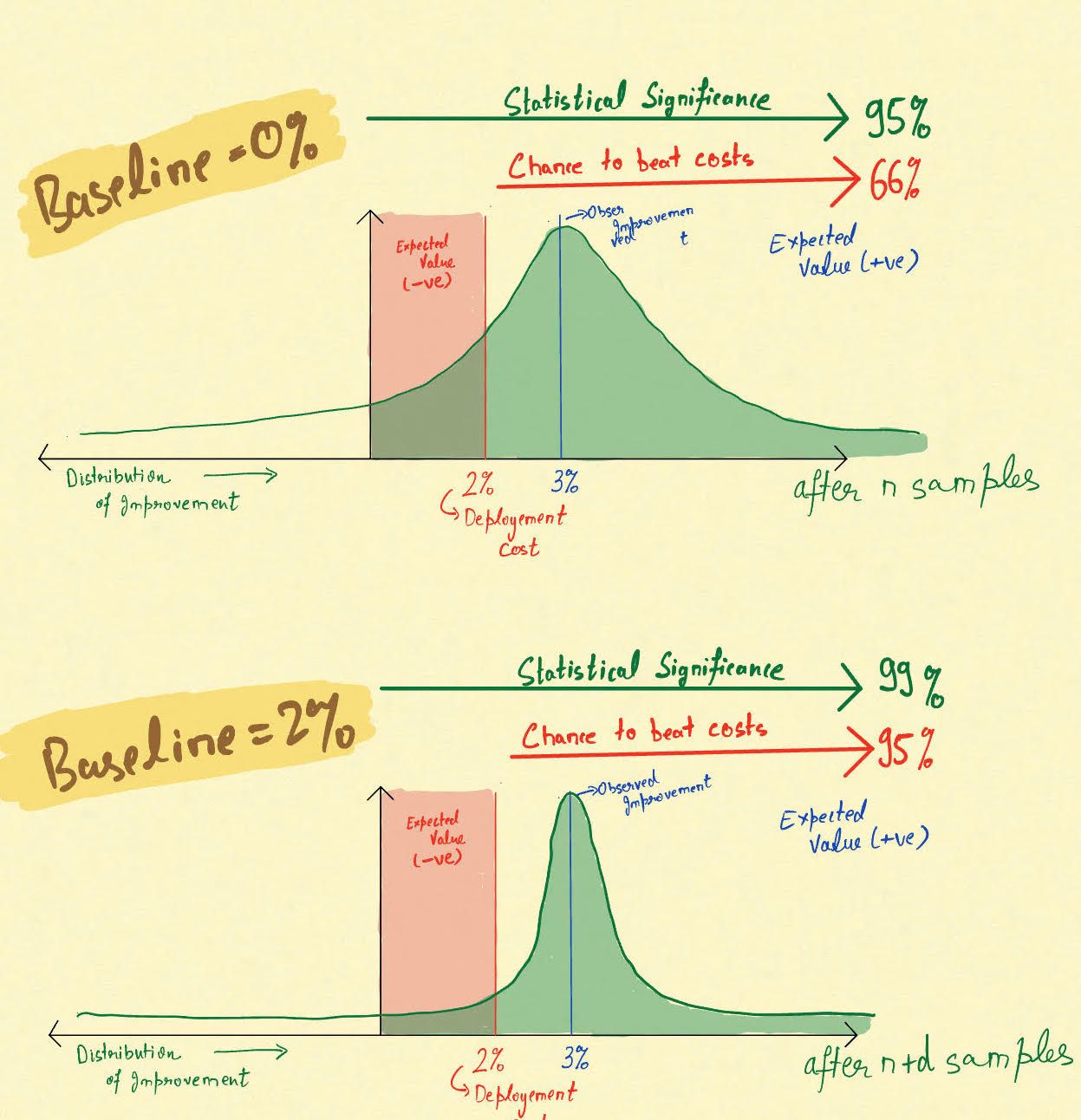
Let us take the example given in the introduction. Suppose your ROPE estimate is 2%. When you calculate significance without ROPE you might get a result that there is a 95% chance that Variation is better than Control and the improvement is 3%. However, at this stage, if you calculate significance with ROPE you will get a probability of only 66%. The question is would you want to deploy this change? The probability it is better than control is 95% but the probability that it will justify your implementation costs is only 66%.

Initially, ROPE and significance might have seem independent concepts but they are not. Unlike MDE, ROPE demands the calibration of significance because now your baseline is not 0. The initial intuition might have been that ROPE and MDE would be the same if enough samples are available. But that is not the case. Once you start calibrating the significance levels according to your new baseline, you would realise that the MDE also shifts according to your new baseline.

In other words, consider a one-sided hypothesis test that tests if the variation performs better than the control or not. Suppose that in 1000 samples, you were able to detect a 5% minimum change (MDE) when the baseline was at 0 (ROPE region was 0). This means that you were not able to detect a difference smaller than 5% in the absence of ROPE. Now, suppose that you introduce a ROPE region below 2% improvement. When you calibrate significance to the ROPE region, MDE also gets shifted accordingly. With the calibrated significance, you will only be able to detect a minimum difference of ROPE + MDE = 7% in 1000 samples.

Success and Guardrail Experimentation

When you start to talk about a region of equivalence, a natural question arises: Having a result better than control makes a case for deploying the feature and having a  result worse than control makes a case for not deploying the feature. But what does the region of equivalence mean? If the change is found to be equivalent, do you deploy the change or not. Trying to answer this question leads to two distinct business use-cases of experimentation.

Let us go back to the case explained in the last paragraph of the previous section to understand the two different business use cases. Note that to calibrate your significance with ROPE, you can essentially do it in two ways. In the first case, you can calibrate with the upper ROPE limit (+2%) and in the second case, you can calibrate with the lower ROPE limit (-2%).

1. Tests for improvement (Success Metrics): The first type of business case in light of upper ROPE is the case where an improvement below 2% does not justify launching the change. In this case, you want to be sure that with 95% chance the improvement lies above the upper ROPE region because the upper ROPE defines your cost limitations. Hence, you calibrate significance levels with the upper ROPE limit. In 1000 samples you will be able to detect a difference that is either > 7% (ROPE + MDE) or < -3% (ROPE - MDE). To detect a smaller MDE, you will need a larger sample size.
2. Tests for maintenance (Guardrail Metrics): The second type of a business case in light of ROPE is the case where a drop up till -2% is okay for you but a decrease larger than that is a problem. For instance, you might be launching a new website design and want that there is a 95% chance that page load time does not go below -2%. In this case, you will calibrate significance with the lower limit of ROPE which is different from the calibration you make in the first case. Hence, in 1000 samples you will be able to detect a difference that is either < -7% (-ROPE - MDE) or > 3% (-ROPE + MDE).

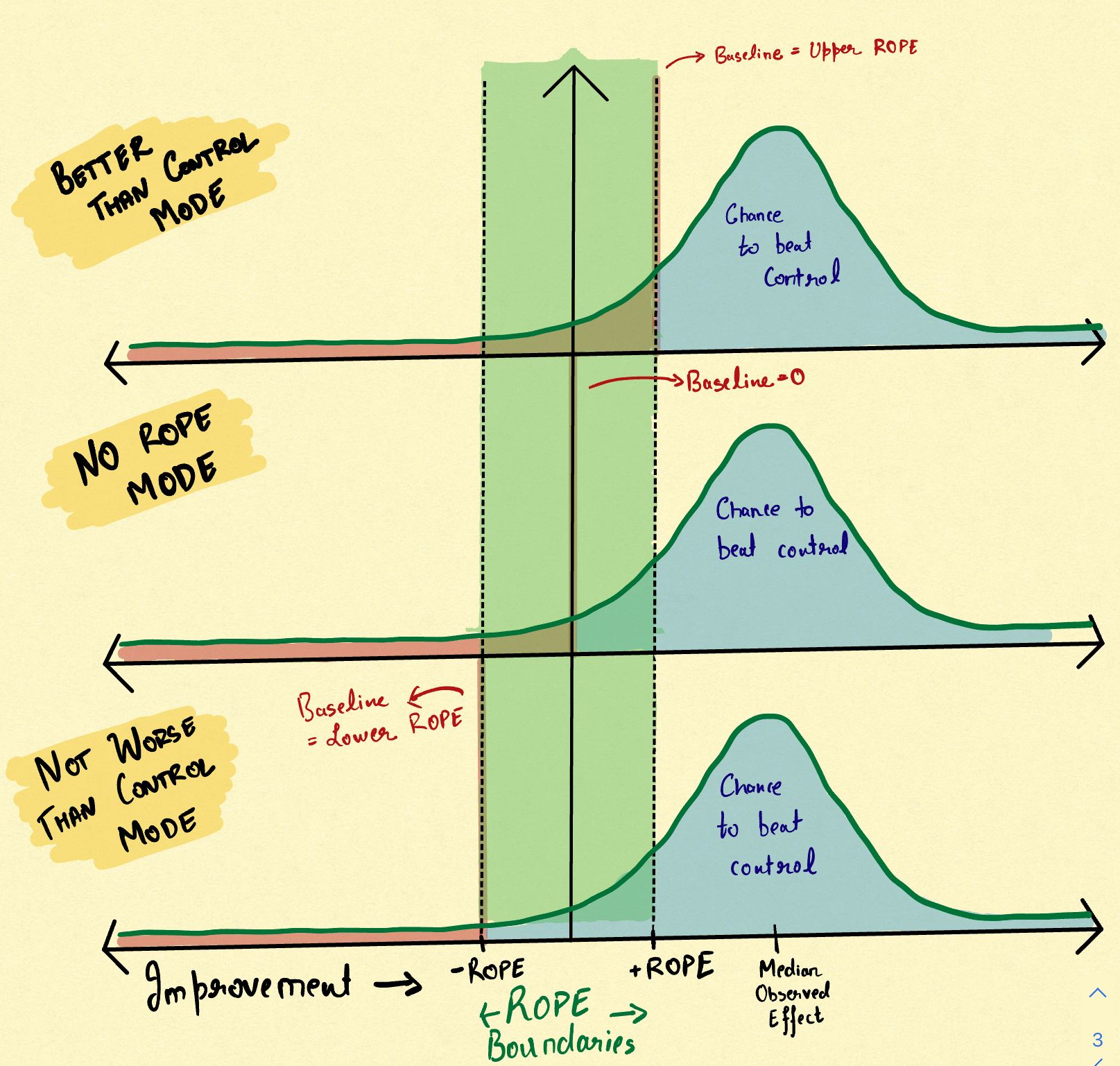
The attached doodle should help you better explain the calibration procedure that I am referring to. One might argue, why do we have to choose one road out of the two and not test for maintenance and improvement simultaneously? Since the two statistical approaches do not demand a separate data collection process, calculating significance via both does not hurt in terms of visitor cost.

The answer is that theoretically yes. In fact, in a given sample size you can only test for a unique MDE but you can test for any number of ROPE regions as you want because shifting the ROPE region does not need any change in the data collection process. However, you must remain careful because making many comparisons inflates the error rates of your analysis. If you try to look for a pattern hard enough, statistics will more likely show you a pattern (Occam's Razor). Hence, if you do decide to introduce ROPE in your calculations, it is best you stick to one ROPE region and even better choose your business case in advance. Either calibrate with the upper limit or the lower limit. If you are doing with both, deploy adjustments for multiple testing.

The way ahead

The topic of ROPE is deep and from here on it leads to the convoluted question of one-way, two-way, or multi-way tests. In a future blog post, I will discuss this topic in detail. To wrap up, ROPE is a nuanced concept that you do not need necessarily in your A/B tests. Most use cases of experimentation do not need a ROPE region because, in the online world, the costs of implementation are usually not very high.

However, understanding ROPE is important because it helps you understand the annoying habit of A/B testing I expressed in the introduction. It is helpful to understand that as the number of samples increases, statistics calls out the smallest of differences to be significant.