The Curse of the False Positives

^{Context: I am now writing a series of blogs on the first thread of discussion in experimentation, The Statistical Nuances in Experimentation. In the next set of blogs, I will write about each point on the statistical nuances.}

Most procedures that seek to segregate instances into positives and negatives are neither perfect nor deterministic. A judge who exercises the best of his judgment to decide if the accused is guilty or not, might still be wrong. A test for pregnancy taken with the most accurate equipment can also be misguiding. Similarly, no matter how meticulously a scientific experiment is planned, the result can end up being wrong. False positives (and false negatives) are a harsh reality of the world that we live in because reality is complex and any procedure to summarise the complexity of the world is essentially just a model.

In the context of experimentation, false positives (also called type-1 errors) are experiments which are declared to be significant when infact they were not. Hence, if in an A/B test, you receive a winner but later realise that the winning variation does not move the goal, you can say that it was a false positive. False negative on the other hand are experiments which did not conclude in statistical significance, but were actually significant. False Positives and False Negatives are partly a consequence of the design your testing procedure, but majorly a consequence of the underlying randomness in the world.

Once you realize that all judgments ever made by an algorithm or a human are vulnerable to the possibility of an error, you start to look at most situations from the lens of false positives and false negatives and the costs associated with them. For instance, many judiciaries around the world prefer to consider an accused innocent as long as they are not proved guilty. On the contrary, other judiciaries prefer to consider an accused guilty until they prove themselves to be innocent. The difference is that by the first heuristic you are able to control for false positives at the cost of false negatives. The idea is that no innocent person should be sent to the gallows even if you set free a few criminals in the process. The image below will help you understand:

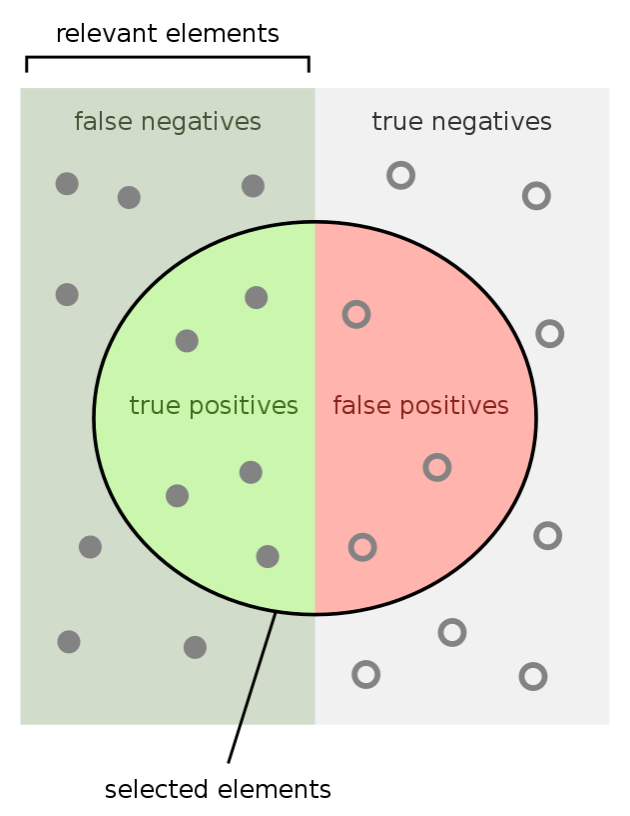
The False-Positive False-Negative Tradeoff

A fundamental thing to realize about false positives and false negatives is that it is very easy to reduce one at the cost of the other. For instance, a judge that never declares anyone a criminal will have a record of never convicting a false positive (declared guilty, actually innocent). Similarly, a Covid test that results in positive for everyone, will have a 0% false-negative rate. But as you see both the judge and the covid-test will be useless in their own way.

Controlling any one of the false-positives or false-negatives is often a trivial problem. The real complexity of statistics (and human judgement for that matter) lies in balancing out false positives and false negatives so that you achieve the maximum accuracy in your decisions. However, as we will see in the next section, often there is an incentive in being biased towards one of these two errors.

All algorithms provide you with a lever to trade off false positives with false negatives. Setting that lever to a perfect choice is the job of a data scientist/statistician. To properly analyze the false positive and the false negative rates of an algorithm, data scientists use a confusion matrix as shown in the figure below. The confusion matrix is in my opinion, the most helpful table to inspect the false-positive and false-negative rates in your methodology.

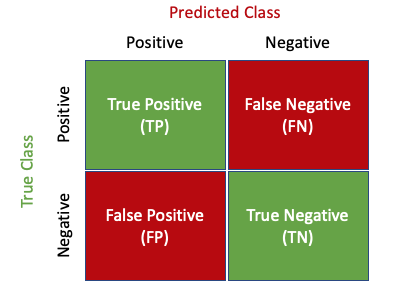
Costs of False Positives and False Negatives

One might think that the optimal procedure should balance out false positives with false negatives equally but this is far from the truth. False Positives and False Negatives often have different costs associated with them. Imagine a patient getting tested for a fatal disease (say AIDS). The cost of a false positive (declared positive, but actually healthy) in this scenario is the panic, the hysteria and the cost that the person incurs in an attempt to treat the disease. However, the cost of a false negative (declared negative, but actually diseased) is the patient walking out of the hospital without realizing that he has a growing disease inside him that might later take his life. Hence, the cost of a false negative is usually much higher in medical tests. Most medical tests hence are biased toward controlling for false negatives rather than false positives because the latter will be caught sooner or later in the diagnosis.

The tradeoff between false positives and false negatives cannot be settled without considering the costs of each in the given context. Most machine learning algorithms create a cost function taking into account the cost of different types of error and then optimise this cost function to tune the hyper-parameters of the algorithm effectively. Hence, whenever you think about false positives and false negatives in a usecase, the next thing to think about is the costs associated with each one.

Relevance in Experimentation

As we read further in experimentation, you will realize that false positives (and false negatives) are caused by a multitude of reasons that are hard to control. Most scientists have to accept the possibility of error in their experiments and strive to mitigate these errors. But as stated earlier, the causes of error are not just restricted to the design of the experiment but to the underlying randomness in the world as well. For instance, observe the following table from a recent paper about A/B Testing Intuition Busters.

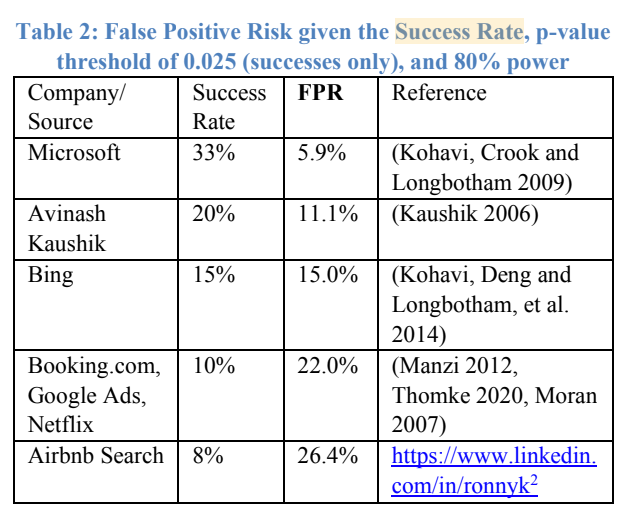
The table shows the relationship between success rate and false positive rates. Success rates are the percentage of good ideas (the ideas that really had an impact on the goal metric) that the experimenter at these companies were generating. False Positive Rates fired up to 26.4% when the percentage of good ideas dropped to 8% in Airbnb. Success rate is one of the metrics that lie outside the control of the procedure and yet impacts false positives so strongly. I plan to write about this phenomena in a future blog on population prevalence.

False Positive Rates are hard to contain. They inflate when you calculate significance more than once. They inflate when you break down the data into groups and calculate significance separately on each group. and they also inflate when the prevalence of the observed phenomena is rare in actuality. Hence, a part of being a scientist is realising that there is always a probability that you are wrong even if you have tested all your hypotheses with data.

In my discussion on the nuances of statistics, false positives and false negatives will be a fundamental statistic of interest as we explore how different things inflate the probability of seeing a pattern just by chance. In the next blog on the statistical nuances, I will talk about the concept of statistical power. Statistical Power will tie the concept of true positives to sample sizes required for the test. Sample Sizes will be another fundamental statistic of interest as we sail through statistical nuances.