The Bayesian vs Frequentist Debate: Future

^{Reference to past blog: In the previous blog on Bayesian vs Frequentists, I explained the major criticisms that both ideologies have faced. In this blog, I majorly present my views on the future of the Bayesian vs Frequentist tussle.}

In this final note on the Bayesian vs Frequentist debate, I would like to share my opinions on the broader context of this debate through time. It is surprising that although the Bayes Rule has been here since 1763, the debate on Bayesian vs Frequentist has never been resolved. Further, it is also surprising to see that proponents of Bayesians are advocating the new science staunchly, yet most of the practical experimentation community is still using p-values comfortably. In this note, I want to express my understanding of these realities.

The core fundamental to understand is that in practice, Bayesians have to generate multiple realities from their probabilistic simulators to calculate backward probabilities. For instance, Nasim Nicholas Taleb is an influential mathematician and trader who used Bayesian MCMC models to make decisions in trading. In his book Fooled By Randomness, he talks about these "Monte Carlo" (just a fancy statistical name for 'randomized') simulators which he used to generate various directions that the stock could have gone into. This helped him retrospect through data and see why his decisions were right or wrong.

Bayesians usually create models expressing their understanding of causality and then sample multiple realities from that model. Out of these generated samples they are able to calculate the posterior probabilities. This fundamental step of generating samples is inate to Bayesian and while smaller models can be solved without samples, large complex models cannot be solved without sampling.

Why were Bayesians stuck?

I believe that since 1763, Bayesians were stuck because they did not have computers to sample millions of realities from their Monte Carlo simulators. With the limit of sampling by hand, Bayesians did not have the luxury to create elaborate models and infer backward probabilities. Frequentists on the other hand were able to solve complex problems as well because p-value calculations were essentially forward probabilities. Unlike backward probabilities, forward probabilities could simply be multiplied by the multiplication rule.

For instance, take the example of two coins. Suppose, a pair of heads have been observed and the question is if the coins were biased or not. The null hypothesis is that the coins were not biased. What is the p-value? Assuming that the coins were not biased, the probability of seeing two heads is 1/2*1/2 = 1/4 (observe the multiplication). However, what is the probability assuming the alternate hypothesis? The alternate hypothesis is that the coins were actually biased.

Bayesians would choose two priors to model the probability of heads on the two coins. Then they would sample through with their two priors and see how many times two heads were observed. With this information, they will update their posteriors about the likely probability of heads on both coins. Do you see the effort Bayesians had to do even to small a simple problem of just two heads?

Without the power of computers, Bayesians could not handle even the smallest of problems because generating samples was impossible by hand. The emergence of computing has given a boost to Bayesian in a way that now even complex models can be easily solved with a probabilistic programming library like PyMC3 or Stan. Now you can simply define a model with variables and in the final layer plug in the ground truth (data). The model learns backward probabilities and updates the join posterior across all variables at once.

The time-tested approach of the Frequentists

Despite these amazing statistical advances in Bayesian, when you look around you see Frequentists to be much more common in all branches of science. Frequentist methodologies have been tested for more than 100 years in multiple branches of science such as drug discovery, psychology, and social sciences. There is no doubt in the fact that no matter how much p-values have been criticized in academics, they are much more common compared to the Bayesian counterpart of the Bayes Factor or the probability to beat baseline.

The Bayesian approach to statistical significance is currently fragmented and unstandardized. As we saw in a previous blog, Bayesians have not one but two entirely different approaches towards significance. The Bayesian approach is currently being handled in different ways through multiple communities of Bayesian advocates.

I believe that in the current age, the penetration of Frequentists in our scientific experimentation is much more deep which renders a deep trust towards the earlier approach. It is upto the Bayesians to probably harness the perceived power of Bayesian Statistics or atleast start to accept if in the absence of priors, the power will remain incremental and mostly theoretical.

Moving beyond p-values

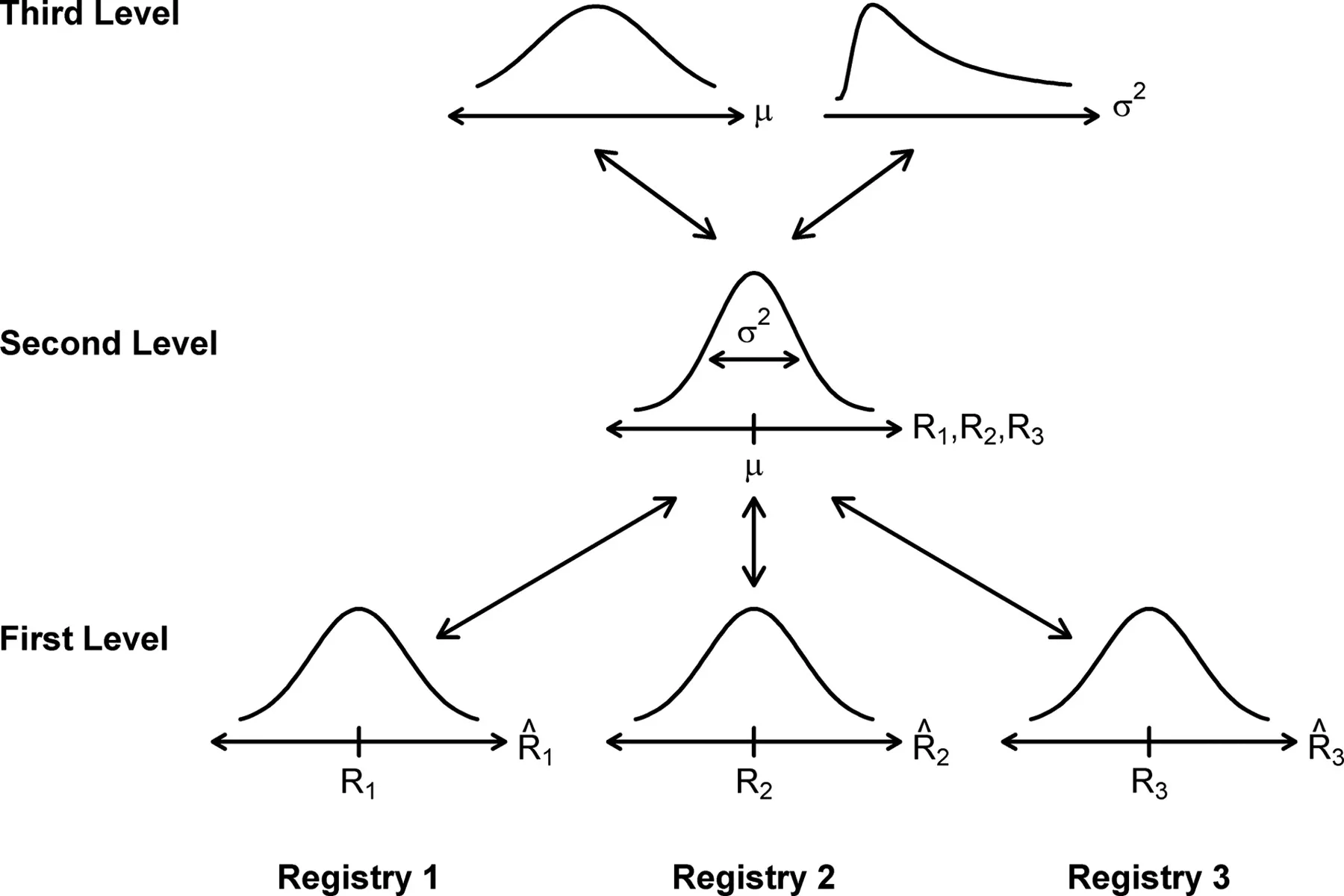
In my personal experience, I have lived through a phase of fascination at the thought that probabilistic machines in the future will not just be generating future predictions but also past retrospections on why something happened as it happened. This I believe is the promise of Hierarchical Bayesian Models.

A good example would be the TrueSkill algorithm embedded into online games that give a score to the capabilities of all players as they play games against each other. Whenever you are playing a team online game on your X-Box, Microsoft's True Skill algorithm is maintaining priors for the performance of each player in the game. It automatically does some complex algorithmic hocus-pocus and updates player scores based on which team won. It is a hierarchical Bayesian model that does all that and it is a great example of a successful Bayesian application to a problem that in my opinion cannot be solved through Frequentist methods. (For a good example, see here how a football match score is being predicted by a Bayesian model).

With the explosion in computing power, I deeply expect more complex problems to be solved with the power of Hierarchical Bayesian Models. Finally, Judea Pearl is a scientist who believes the power of Bayesian to solve the most fundamental problem of science with statistics.

Judea Pearl believes that statistics and machine learning as a whole needs to move towards not just identifying correlations between input and output but at understanding why something happens the way it happens. The Book of Why explores the question of finding causality through observational data using Bayesian models.

Observe that currently we run controlled experiments to infer causality. Judea Pearl believes that the apex of AI would be the ability to infer causality from just observational data. Observational data is the data collected just from the environment without the need of running a controlled experiment. In slightly hyperbole words, one can say that the dream would be to automate the scientific procedure.

On this note, I would like to end the debate on Bayesian vs Frequentists and tie the various threads that we have studied towards a discussion on practical experimentation and its problems.

Note: My blog probably only explores the future of the Bayesian side of the debate. Currently, there is a lack in my understanding of how Frequentists have evolved which I am filling with the help of LinkedIn friends like Geoffrey Johnson, Graeme Keith, and Valeriy M. Once I understand that debate, I will try and throw light on the evolution of the Frequentist side of the debate.