The Bayesian Vs Frequentist Debate: Criticisms

^{Reference to past blog: In the previous blog in this series, I explained the uniquenesses of both the Bayesian and the Frequentist ideologies. In this blog, I discuss the criticisms that both have faced in the Bayesian vs Frequentist debate.}

The Bayesian vs Frequentist debate has seen its way through academic journals, online critiques, coffee shops, and even domestic banters. An instance of this debate can be seen in the comments of my LinkedIn Post on Bayesian Statistics. It seems like Bayesian lovers are staunch advocates, Frequentists say they have evolved much further to newer methods. But both have their own criticisms of the other side. In this blog, I intend to explore the major criticism in my understanding that each ideology faces.

Bayesians are often criticised for their subjectivity and their need for defining a prior which a lot of times is not available. Frequentists on the other hand face flak in the statistical community for the in-famous p-values.

I am certain that these are not the only criticisms that both sides face. But I attempt to explain the two major criticisms that I have observed up till now.

P-values: What do they even mean?

P-values have been interpreted wrongly by many scientific studies over the year. The fundamental misunderstandings about p-values usually are of the following types:

1. Assuming p-values to be the backward probability rather than the forward probabilities: Many have often interpreted the p-value as the probability that the null hypothesis is true. The truth is that p-values are not the probability of the null hypothesis being true (backward probability), but the probability of the observed data assuming the null hypothesis (forward probability). P-values by construct can never be the probability of the cause. So, if ever you find yourself confused remind yourself that the p-value can only be the probability of the effect.
2. Assuming that (1 - p-value) is the backward probability of the alternate hypothesis being true: Since the p-value was not the probability of the cause in the first place, you cannot subtract it from 1 and get the probability of the alternate hypothesis. This cardinal sin has been committed time and again and a poor lady, Sally Clark, was convicted of murdering her two sons in 1999, just because of this error.
3. Assuming that (1 - p-value) is the probability of observing the data assuming the alternate hypothesis: A related error many scientific studies have made is assuming that the forward probability of data from the Null Hypothesis and the forward probability of data from the alternate hypotheses will always sum to 1. This is far from the truth. The blog on the Bayesian alteration gives an example to show that the two probabilities might not sum up to 1.

Pertaining to the misinterpretations above, many scientists have often twisted p-values to their convenience and many have reached the wrong conclusions due to the same. P-values also have a unique limitation of not being valid before a certain number of samples are collected. In the domain of A/B testing where people run a test and start observing the statistics while the data is being collected, many have made the error of trusting premature p-values and closing the test once at the first instance of statistical significance.

It is safe to say that because of the reasons above, p-values is never the favorite part of the debate for Frequentists. Lacking the framework and the understanding of backward probabilities, to the best of my knowledge Frequentists have stuck with p-values ever since.

Priors: Where do we even find them?

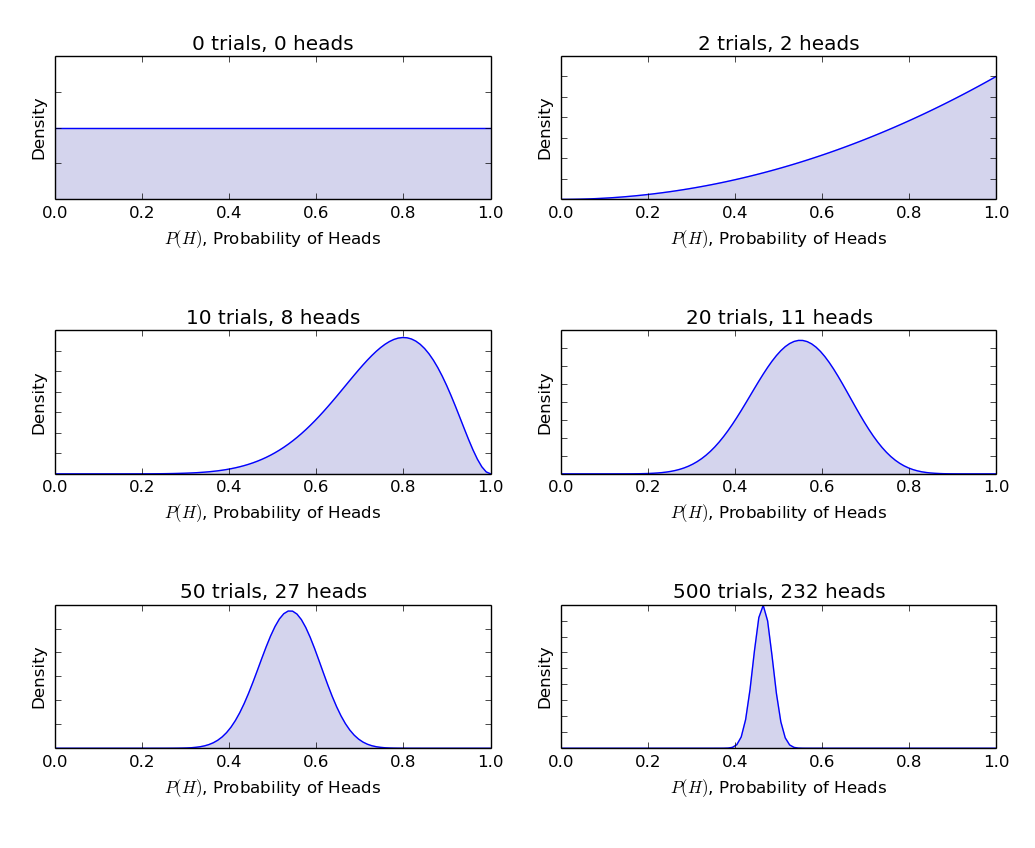
Let's face it the concept of priors was a theoretical genius to solve the problem of backward probabilities but practically finding the right prior is much more difficult than it sounds. I have started to realize that priors are mostly made up of latent information that is very hard to gather in the first place. The prevalence of a disease, the rate at which a digital marketer generates good ideas and the probability of the sun exploding (a reference to the joke in the previous post) are all questions not very easy to answer. More scary is the fact that any wrong information stuffed inside these priors will also bias the learnings from actual empirical data.

Hence, Bayesians have put a great deal of effort into developing uninformative flat priors which they claim do not bias the learnings from empirical data. These priors are the ones that are used in most statistical procedures to date. However, Frequentists have often claimed that there is no truly uninformative prior and all priors bias the results to an extent. Frequentists usually choose to go with their methods over choosing a Bayesian prior and biasing their results.

Bayesians have often been rigorous enough to gather trustworthy priors by analyzing past studies and that attempt has worked to an extent. However, for a layman trying to calculate statistical significance using Bayesian methods, it is often a headache to find a good prior.

Bayesians have hence been criticised for their subjectivity and the need for extra information before doing Bayesian calculations. Most Bayesian frameworks use an uninformative prior in practice and often end up reaching the same conclusions as the Frequentists as well.

Frequentists then say, if we are to use an uninformative prior and reach the same conclusions as a Frequentist, then why go through the masquerade?

The way ahead

In this blog, I have highlighted the two crucial criticisms that are faced by both Frequentists and Bayesians. In the next blog, I plan to write about the current state of the Bayesian vs Frequentist debate before finally closing the debate on Bayesian vs Frequentist and moving on to common problems of A/B testing and experimentation that are faced by both the communities.